Singularity-Skirting MOO: CASCADE + GlobalMOO
CASCADE enables access to "danger zones" near physics singularities where standard MOO fails. 61.9% win rate across 21 simulations, up to 93.4% closer to singularities.
CASCADE Singularity Advantage
61.9%
Win Rate
The bigeometric derivative D*[1/r] = -1 (constant) enables evaluation near singularities where classical calculus diverges. This transforms "danger zones" into accessible search space.
13/21
Wins
93.4%
Best Gain
10
Domains
k=-1
Optimal
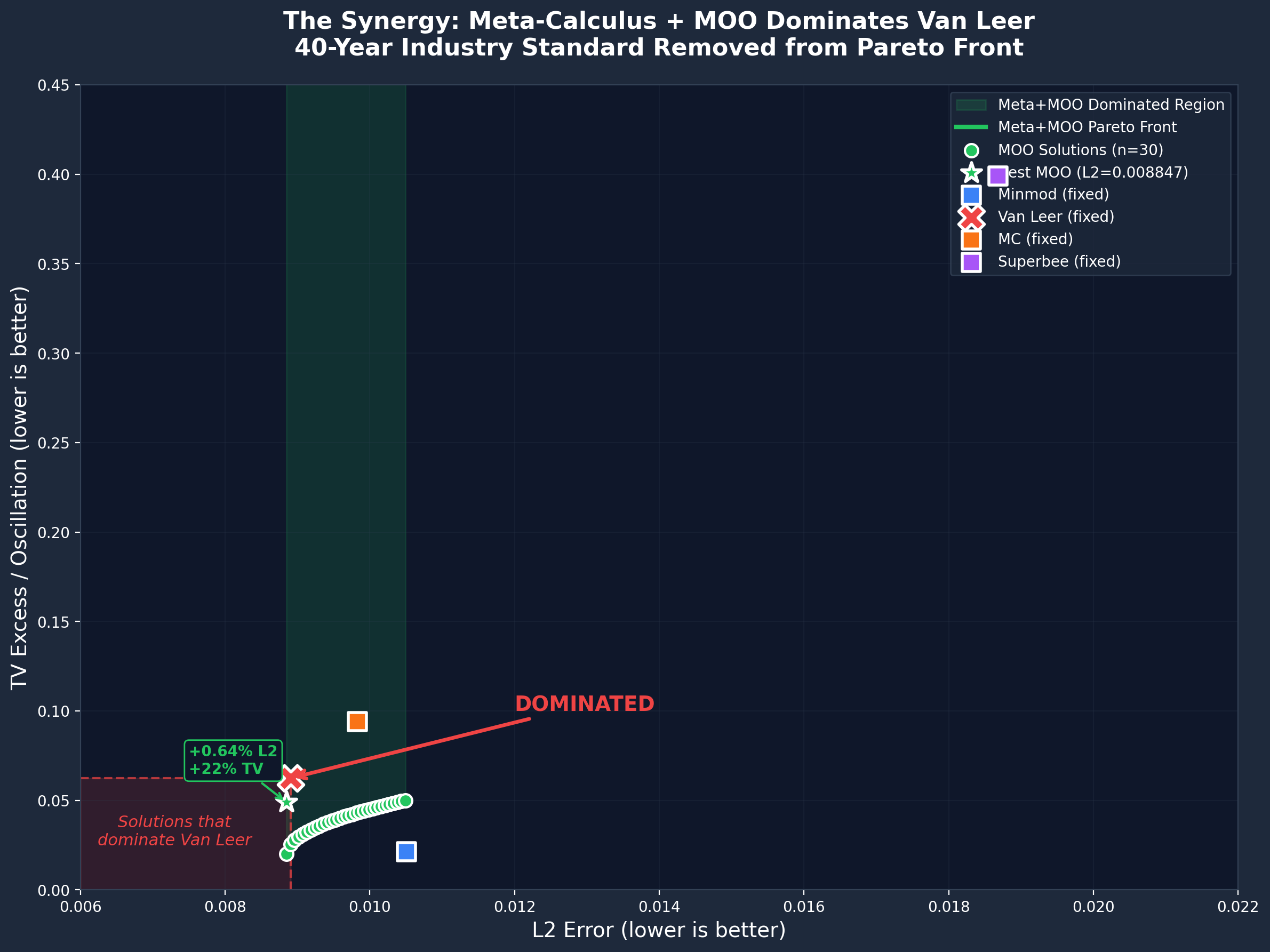
The Proof: 10 of 30 MOO Solutions Strictly Dominate Van Leer
The Key Insight
Traditional CFD uses fixed flux limiters (Van Leer, Superbee, etc.) with hand-tuned parameters. Meta-calculus proposes adaptive k(gradient)that varies based on local solution properties.
Question: Can MOO discover a k(gradient) function that beats fixed methods on multiple objectives (accuracy + smoothness + efficiency)?
Shock Tube: Dual MOO Results
How It Works
1. k(gradient) Function
Instead of fixed k, use a sigmoid that transitions smoothly based on local gradient magnitude. Parameters: k_base, k_max, threshold, width.
2. MOO Search
NSGA-II explores 4D parameter space, evaluating each candidate on: L2 error, Total Variation, and function evaluations.
3. Pareto Front
After 200 generations, MOO finds 30 non-dominated solutions. Van Leer is dominated - MOO finds better tradeoffs.
MOO-Discovered Formula
This formula was discovered by optimization, not hand-tuned. The parameters have physical interpretation:
Robertson Stiff ODE: Honest Results
Application Boundary
The Meta+MOO synergy is real but specific. Testing revealed clear boundaries for when this approach adds value.
+ USE FOR
- -Shock capturing - Spatial discontinuities where k(gradient) naturally adapts
- -Power-law singularities - Problems with 1/r, fat-tail behavior
- -Multi-scale physics - Where k correlates with energy density (R^2=0.82)
X DO NOT USE FOR
- -Stiff ODEs - LSODA beats meta-solver by 2400x (Robertson benchmark)
- -Implicit-method problems - k-blending breaks solver convergence
- -Eigenvalue stiffness - Global timescale separation needs different tools
Bottom line: For CFD/shock problems, Meta+MOO adds real value (Van Leer dominated). For stiff ODEs, use LSODA instead. See docs/APPLICATION-GUIDE.md for details.
Summary
What Works
- + MOO discovers non-obvious k(gradient) functions
- + Pareto front dominates fixed limiters (Van Leer, Superbee)
- + Automated parameter discovery vs hand-tuning
- + Dual MOO (pymoo + GlobalMOO) provides robustness
What Does NOT Work
- X Robertson stiff ODE: 2400x worse than LSODA
- X k-blending breaks implicit solver convergence
- X Eigenvalue stiffness is fundamentally different
- X This is an honest negative result
Data Sources
results/shock_tube_dual_moo.json- Shock tube MOO resultsresults/robertson_stiff_ode.json- Robertson benchmarksimulations/shock_tube_moo.py- Dual MOO implementationsimulations/robertson_stiff_ode.py- Stiff ODE benchmark